Rumus Web mengumpulkan materi Rumus Trigonometri ini untuk anak SMP SMA demi UAN SNMPTN SPMB SIMAK UI. Silakan dipelajari 

Rumus trigonometri umum
Sudut-Sudut Istimewa sin cos tan 0 30 45 60 90 derajat
Aturan sin cos tan lain
Rumus-rumus Trigonometri pada segitiga dengan sisi a b c
Aturan sinus
Aturan Cosinus
Luas Segitiga 2 sisi dan 1 sudut
Luas segitiga dengan 3 sisi akan dibahas lain waktu
Rumus jumlah 2 sudut trigonometri sin cos tan
sepertinya gambar ini ada yang salah, nanti diperbaiki
Sudut 2A atau sin 2x, cos 2x, tan 2x
Rumus kali trigonometri sin cos cos sin cos cos -sin sin
Rumus jumlah 2 trigonometri sin cos cos sin cos cos -sin sin
Persamaan Trigonometri mudah sekali dikerjakan
Bentuk a Cos x + b Sin x = k cos x-teta
Bentuk a Cos x + b Sin x = c
Nilai Maksimum dan Minimum Fungsi f(x) =a Cos x + b Sin x
yang ini sering juga keluar di soal snmptn
Semoga bermanfaat 
Nov 19, 2012 -  Uncategorized
Uncategorized  Komentar Dimatikan
Komentar Dimatikan
 Uncategorized
Uncategorized  Komentar Dimatikan
Komentar DimatikanYiha Titik Cerah Jawaban ADT
Fungsi rasional dan asimtot
Apa itu fungsi rasional. Fungsi rasional adalah fungsi yang berbentuk 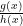 , dimana
, dimana 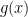 dan
dan 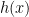 adalah suatu fungsi polynomial. Dan
adalah suatu fungsi polynomial. Dan 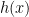 bukan nol. Domain dari fungsi polynomial ini adalah semua nilai x bilangan real kecuali nilai x yang mengakibatkan
bukan nol. Domain dari fungsi polynomial ini adalah semua nilai x bilangan real kecuali nilai x yang mengakibatkan 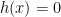 .Contoh fungsi rasional,
.Contoh fungsi rasional, 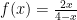
Fungsi tersebut adalah fungsi rasional. Dengan penyebut suatu fungsi polynomial yang bisa sama dengan nol. Domain dari fungsi ini adalah semua bilangan real kecuali suatu nilai x yang menyebabkan penyebut bernilai nol. Domainnya seluruh bilangan real, kecuali 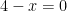 , kecuali
, kecuali 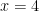 .
.
Karena untuk 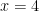 , maka akan terjadi pembagian dengan nol. Ini akan menyalahi aturan. Lalu, gambar fungsinya adalah sebagai berikut.
, maka akan terjadi pembagian dengan nol. Ini akan menyalahi aturan. Lalu, gambar fungsinya adalah sebagai berikut.
Perhatikan gambar grafik tersebut. Gambar grafik tersebut untuk  maka nilai y yang memenuhi adalah sangat besar. Dan untuk
maka nilai y yang memenuhi adalah sangat besar. Dan untuk  , nilai dari y juga akan mendekati tak hingga. Untuk nilai
, nilai dari y juga akan mendekati tak hingga. Untuk nilai 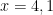 juga demikian. Nilainya akan semakin mendekati minus tak hingga jika nilai
juga demikian. Nilainya akan semakin mendekati minus tak hingga jika nilai 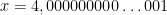 .
.
Inilah yang akan ada hubungan dengan asimtot. Garis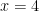 , ini disebut sebagai asimtot tegak (vertical asymptote) untuk gambar grafik ini. Dan garis
, ini disebut sebagai asimtot tegak (vertical asymptote) untuk gambar grafik ini. Dan garis  yang didekati oleh kurva menuju tak hingga, juga merupakan asimtot, yaitu asimtot datar. Jika mengetahui gambar grafiknya, kita akan sangat mudah untuk menentukan asimtotnya, bagaimana kalau tidak diketahui gambar grafiknya? Apakah kita harus menggambarnya dulu atau bagaimana?
yang didekati oleh kurva menuju tak hingga, juga merupakan asimtot, yaitu asimtot datar. Jika mengetahui gambar grafiknya, kita akan sangat mudah untuk menentukan asimtotnya, bagaimana kalau tidak diketahui gambar grafiknya? Apakah kita harus menggambarnya dulu atau bagaimana?
Inilah yang akan ada hubungan dengan asimtot. Garis
Untuk mencari asimtot tegak, yang harus kita perhatikan adalah penyebut dari fungsi rasional tersebut. Ingat!Mencari asimtot tegak untuk fungsi yang di atas, kita tiggal membuat penyebutnya sama dengan nol. Tetapi ingat, beberapa fungsi rasional memang tidak mempunyai asimtot tegak. Misalnya saja suatu fungsi rasional yang mempunyai penyebut 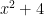 , bentuk ini tidak mungkin sama dengan nol. Sehingga suatu fungsi rasional yang berpenyebut seperti ini (atau yang lain, yang tidak bisa sama dengan nol), tidak akan mempunyai asimtot tegak.
, bentuk ini tidak mungkin sama dengan nol. Sehingga suatu fungsi rasional yang berpenyebut seperti ini (atau yang lain, yang tidak bisa sama dengan nol), tidak akan mempunyai asimtot tegak.
Untuk mencari asimtot datar (horizontal asymptote), Perhatikan aturan berikut :
Pertama, Jika pangkat tertinggi pada pada pembilang sama dengan pangkat tertinggi pada penyebut, maka asimtot datarnya ada di garis y sama dengan koefisien pangkat tertinggi pembilang per koefisien pangkat tertinggi penyebut.
Secara umum, jika fungsinya adalah 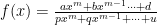 ,
,
maka asimtot datarnya ada di 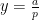
dengan m adalah pangkat teetinggi dari kedua polynomial tersebut. (polynomial sebagai pembilang dan polynomial sebagai penyebut)
dengan m adalah pangkat teetinggi dari kedua polynomial tersebut. (polynomial sebagai pembilang dan polynomial sebagai penyebut)
Misalnya, asimtot datar dari fungsi rasional berikut ini
Asimtot datarnya adalah 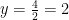
Kedua, jika pangkat terbesar pada pembilang lebih kecil dari pada pangkat terbesar pada penyebut, maka asimtot datarnya ada di 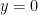
Secara umum, jika fungsinya adalah 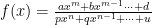 , dengan <img title=”m<n” src=”http://s0.wp.com/latex.php?latex=m%3Cn&bg=ffffff&fg=000000&s=0″ alt=”m
, dengan <img title=”m<n” src=”http://s0.wp.com/latex.php?latex=m%3Cn&bg=ffffff&fg=000000&s=0″ alt=”m
maka asimtot datarnya ada di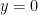
maka asimtot datarnya ada di
Jika pangkat terbesar pada pembilang lebih besar dari pada pangkat terbesar pada penyebut, maka tidak ada asimtot datar. Ingat!
Asimtot miring (oblique asymptote atau slant asymptote) bisa didapatkan untuk kasus yang terakhir ini.
Asimtot miring (oblique asymptote atau slant asymptote) bisa didapatkan untuk kasus yang terakhir ini.
Misalnya saja fungsi berikut ini :
Untuk mencari asimtot dari grafik tersebut, maka lakukan pembagian antara pembilang dan penyebut. Akan ada hasil pembagian dan sisa, seperti berikut :
Sekarang bisa kita lihat, ketika x menuju tak hingga, maka 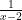 menuju nol.
menuju nol.
Dan nilai 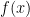 sama dengan
sama dengan  . Inilah yang bisa menyimpulkan bahwa, grafik kurva pada soal, akan mendekati garis
. Inilah yang bisa menyimpulkan bahwa, grafik kurva pada soal, akan mendekati garis 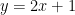 ketika x menuju tak hingga.
ketika x menuju tak hingga.
Asimtot miringnya pun didapatkan yaitu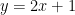 ,
,
Ingat, tidak ada asimtot datar.
Asimtot miringnya pun didapatkan yaitu
Ingat, tidak ada asimtot datar.
Asimtot tegak ada di 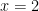 , karena nilai inilah yang menyebabkan penyebut sama dengan nol.
, karena nilai inilah yang menyebabkan penyebut sama dengan nol.
Seperti pada gambar berikut :
Asimtot datar tidak ada ketika pangkat terbesar dari pembilang lebih besar dari pangkat terbesar dari penyebut. Ingat. Sehingga ini menyebabkan, tidak mungkin adanya suatu fungsi yang mempunyai asimtot datar dan asimtot miring secara bersamaan.
http://andika27.blog.com/2012/11/20/materi-trigonometri/
















Tidak ada komentar:
Posting Komentar